@notsosureofit Hypothesis
The proposition that dispersion caused by an accelerating frame of reference implied an accelerating frame of reference caused by a dispersive cavity resonator. (to 1st order using massless, perfectly conducting cavity)
Basic Expression
Starting with the expressions for the frequency of a cylindrical RF cavity [1]:
[math]f = \cfrac{c}{2π}\sqrt{(\cfrac{X}{R})^2+(\cfrac{pπ}{L})^2}[/math]
where "c" is the speed of light in the medium (the speed of light in vacuum divided by the square root of the product of the relative magnetic permeability times the relative electric permittivity of the medium).
For TM modes, X = X[sub m,n] = the n-th zero of the m-th Bessel function. [1,1]=3.83, [0,1]=2.40, [0,2]=5.52 [1,2]=7.02, [2,1]=5.14, [2,2]=8.42, [1,3]=10.17, etc.
and for TE modes, X = X'[subm,n] = the n-th zero of the derivative of the m-th Bessel function. [0,1]=3.83, [1,1]=1.84, [2,1]=3.05, [0,2]=7.02, [1,2]=5.33, [1,3]=8.54, [0,3]=10.17, [2,2]=6.71, etc.
- Here is a table [2] to 15 digits precision for the roots of the cylindrical Bessel functions X[sub m,n] and for the roots of its derivative X'[subm,n] from m=0 to m=10, and from n=1 to n=5
Rotate the dispersion relation of the cavity into doppler frame to get the Doppler shifts, that is to say, look at the dispersion curve intersections of constant wave number instead of constant frequency.
[math]\Delta f = \cfrac{1}{2f}(\cfrac{c}{2π})^2X^2(\cfrac{1}{Rs^2}-\cfrac{1}{Rb^2})[/math]
This is a cylindrical approximation and could be replaced with a tapered dielectric index of refraction in a cylindrical cavity.
and from there the expression for the acceleration g from:
[math]g = \cfrac{c^2}{L}\cfrac{\Delta f}{f}[/math]
such that:
[math]g = \cfrac{c^2}{2Lf^2}(\cfrac{c}{2π})^2X^2(\cfrac{1}{Rs^2}-\cfrac{1}{Rb^2})[/math]
This is the acceleration at which the dispersion of the tapered cavity is balanced out by the dispersion due to its acceleration.
Using the "weight" of the photon in the accelerated frame from:
[math]W = \cfrac{hf}{c^2}g[/math]
where we make the connection via the Equivalence Principle that the acceleration of a photon seen in the rest frame is that which is balanced out in the accelerated frame. That is, the dispersion of the tapered cavity reduces to zero (along the axis) in that accelerated frame of reference.
Such that:
[math]W = T = \cfrac{h}{L}\Delta f[/math]
We identify that as the thrust per photon:
[math]T = \cfrac{h}{2Lf}(\cfrac{c}{2π})^2X^2(\cfrac{1}{Rs^2}-\cfrac{1}{Rb^2})[/math]
Notice that this is the static thrust per photon in a rest (un-accelerated) frame traveling with the cavity. That is to say, thrust is dependent on the acceleration that the physical cavity experiences and goes to zero at the acceleration g. This is an example of a negative feedback system where the steady state acceleration in the cavity frame of a free cavity will always be less than that calculated from the static force. It has no dependence on the linear velocity. (The case of circular motion is different in that the centrifugal "force" is dependent on angular velocity and will further negatively affect the thrust.)
If the number of photons is
[math]\cfrac{P}{hf}(\cfrac{Q}{2πf})[/math]
then the total thrust is
[math]NT = \cfrac{PQ}{4πLf^3}(\cfrac{c}{2π})^2X^2(\cfrac{1}{Rs^2}-\cfrac{1}{Rb^2})[/math]
or
[math]NT = \cfrac{2PQ}{L(2πf)^3}(c X)^2 (\cfrac{1}{Ds^2}-\cfrac{1}{Db^2})[/math]
or
[math]NT=\cfrac{2PQ}{L ω^3}(c X)^2 (\cfrac{1}{Ds^2}-\cfrac{1}{Db^2})[/math]
where Ds = diameter at small end, Db = diameter at big end and ω = angular frequency.
Example
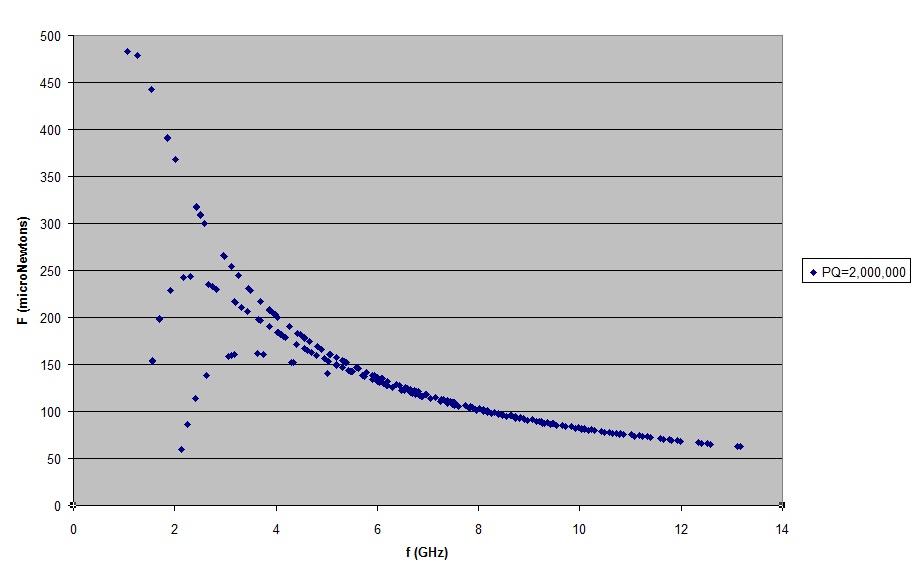
Here is an example of the force of each mode vs frequency for m = 0 to 10, n = 1 to 5, p = 1 to 3 from the table referenced above.
In this case Rs = 0.0794 m, Rb = 0.1397 m, L = 0.2286 m (the dimensions of the truncated cone cavity tested at NASA Eagleworks as reported by Brady et.al.) and PQ = 2*10^6 watts.
The three curves represent p=1, p=2 and p=3, where p is the quantum number in the longitudinal direction, for modes [math]TM_{mnp}[/math] and [math]TE_{mnp}[/math].
For constant geometrical dimensions, and constant quality factor and input power, the asymptotic behavior of thrust is inversely proportional to the cube of the frequency and proportional to the square of X.
Appendix 1
Proof that scaling dimensions inversely proportional to frequency keeps the thrust invariant:
Suppose that the thrust at frequency [math]f_1[/math], and dimensions [math]L_1[/math], [math]Ds_1[/math], and [math]Db_1[/math] is
[math]NT_1 = \cfrac{2PQ}{L_1(2πf_1)^3}(c X)^2 (\cfrac{1}{Ds_1^2}-\cfrac{1}{Db_1^2})[/math]
then, at frequency [math]f_2[/math] a multiple of frequency [math]f_1[/math]
[math]f_2 = n f_1 [/math]
where the frequency ratio
[math]n=\cfrac{f_2}{f_1} [/math]
can be any irrational number (not equal to zero). Scaling dimensions to be inversely proportional to the frequency ration n:
[math]L_2=\cfrac{L_1}{n} [/math]
[math]Ds_2=\cfrac{Ds_1}{n} [/math]
[math]Db_2=\cfrac{Db_1}{n} [/math]
and substituting, we get the thrust for frequency [math]f_2[/math] and dimensions [math]L_2[/math], [math]Ds_2[/math], and [math]Db_2[/math] to be:
[math]NT_2 = \cfrac{2PQ}{L_1(2πf_1 n)^3}(c X)^2 (\cfrac{1}{(\cfrac{Ds_1}{n})^2}-\cfrac{1}{(\cfrac{Db_1}{n})^2})[/math]
and since the factor of [math]n^3[/math] occurs both in the numerator and the denominator, it cancels out, leaving
[math]NT_2 = NT_1[/math]
If the mode shape is kept invariant, for constant quality factor and input power, the thrust force is invariant, independent of frequency when the diameter and the length of the cavity are both scaled to change inversely proportional to the frequency ratio n.
Appendix 2
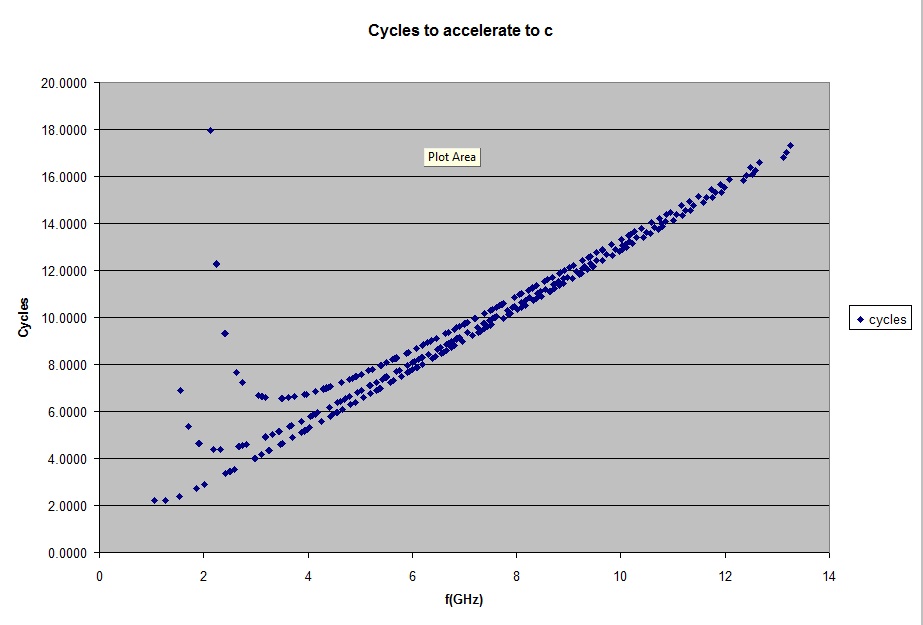
An interesting expression to examine is [math]\cfrac{fc}{g} [/math]
It represents the number of cycles for the photons in the cavity to reach velocity c if they were free to do so at the acceleration g.
In that respect [math]\cfrac{g}{fc} [/math] represents a degree of coupling between the standing waves in the cavity and a traveling wave.
In this case Rs = 0.0794 m, Rb = 0.1397 m, L = 0.2286 m (the dimensions of the truncated cone cavity tested at NASA Eagleworks as reported by Brady et.al.) and PQ = 2*10^6 watts.
The three curves represent p=1, p=2 and p=3, where p is the quantum number in the longitudinal direction, for modes [math]TM_{mnp}[/math] and [math]TE_{mnp}[/math].
Notice that for a cylindrical cavity, it takes an infinite number of cycles for the photons in the cavity to reach velocity c (if they were free to do so at the acceleration [math]g[/math]). For a cylindrical cavity [math]\Delta f[/math] is zero (since the the diameters at both ends are the same, and therefore there is no gradient in that case), which means that the acceleration [math]g[/math] is zero. Hence the number of cycles [math]\cfrac{fc}{g}[/math] approaches infinity for a cylindrical cavity.